数学建模教程

Cherzing2024年8月8日大约 10 分钟

教程

数学建模题型类型

预测类

指通过分析已有的数据或者现象，找出其内在发展规律，然后对未来情形做出预测的过程。
根据已知条件和求解目的，往往将预测类问题分为：小样本内部预测，大样本内部预测，小样本未来预测，大样本随机因素或周期特征的未来预测，大样本的未来预测。

解决预测类赛题的一般步骤：

确定预测目标：
收集、分析资料；
选择合适的预测方法进行预测：
分析评价预测方法及其结果；
修正预测结果；
给出预测结果

算法选择：

评价类

指按照一定的标准对事物的发展或者现状进行划分的过程在数学建模中题点可体现在对生态环境，社会建设，方案策略等进行评价。评价类赛题往往没有明确的指标体系和评价标准，往往是需要查阅各类资料进行构建的，因此评价类赛题也没有明确的答案
赛题分析：解决评价类赛题的关键是指标体系的构建，构建完评价体系后在选择合适的评价方法即可，体系建立应秉承全面，准确，独立的三要素

解决评价类赛题的一般步骤：

明确评价目的：
确定被评价对象；
建立评价指标体系
确定各指标相对应的权重系数；
选择或构造综合评价模型；
计算各系统的综合评价值
给出综合评价结果，

机理分析法

所机理分析是根据对现实对象特性的认识，分析其因果关系，找出反映内部机理的规律。在求解机理分析类问题时首先需要探寻与问题相关的物理，化学，经济等相关的知识，然后通过对已知数据或现象的分析对事物的内在规律做出必要的假设，最后通过构建合适的方程或关系式对其内在规律进行数值表达
赛题分析：机理分析立足于建立事物内部的规律，相对于其他类型的赛题均有章可循，机理分析类赛题往往需要结合众多关联知识才可以进行求解，如空气动力学，流体力学，热力学等

优化类

指在现有现有条件固定的情况下，如何使目标效果达到最佳。如在一座城市公交车公司拥有的公交车数量是固定的，问如何安排线路能够使盈利达到最高。优化类问题往往需要分析三个关键因素：目标函数，决策变量和约束条件，三者往往缺一不可。
赛题分析：解决优化类赛题必须知道优化的目的，约束的条件和所求解的关键变量，需要有较强的编程能力和赛题分析挖掘能力

解决预测类赛题的一般步骤：

确定优化目标；
确定决策变量
构建目标函数；
根据已知条件构建约束条件；
选择合适的方法求解目标函数；
给出优化结果

算法

线性规划问题

示例：

:::code-tabs

@tab text

目标函数 MAX：Z = 2x₁ + 3x₂ - 5x₃

@tab text

约束条件：

1. x₁ + x₂ + x₃ = 7 （等于约束）
2. 2x₁ - 5x₂ + x₃ >= 10 （大于等于约束）
3. x₁ + 3x₂ + x₃ <= 12 （小于等于约束）
4. x₁, x₂, x₃ >= 0 （非负约束）

:::

代码：

from scipy.optimize import linprog
"""
    已知等式Z=2x_{1}+3x_{2}-5x_{3}，
    约束条件为
    x_{1}+x_{2}+x_{3}=7;
    2x_{1}-5x_{2}+x_{3}>=10;
    x_{1}+3x_{2}+x_{3}≤12;
    x_{1},x_{2},x_{3} ≥0，
    求出当Z最大时，x_{1},x_{2},x_{3}的值
"""
# 目标函数的系数
c = [-2, -3, 5]  # 注意，我们取的是-Z的系数，因为linprog默认是求最小值问题

# 约束条件的系数矩阵（A_ub是不等式约束，A_eq是等式约束）
A_ub = [[-2, 5, -1], [1, 3, 1]]  # 大于等于和小于等于的约束
b_ub = [-10, 12]  # 对应的大于等于和小于等于约束的右侧值

# 等式约束
A_eq = [[1, 1, 1]]
b_eq = [7]

# 变量的边界（非负约束）
bounds = [(0, None), (0, None), (0, None)]

# 解决线性规划问题
result = linprog(c, A_ub=A_ub, b_ub=b_ub, A_eq=A_eq, b_eq=b_eq, bounds=bounds)

print(result.x, result.fun * -1)  # 输出解和最大化后的Z值

linprog函数：

scipy.optimize.linprog(c, A_ub=None, b_ub=None, A_eq=None, b_eq=None, bounds=None, method='highs', options=None)

参数说明c: array_like 目标函数的系数，用于构建目标函数c @ x，其中@ 表示矩阵乘法。如果目标是最大化目标函数，可以将c 的元素取反。A_ub: array_like, optional 不等式约束的系数矩阵。每一行对应一个不等式约束A_ub @ x <= b_ub。b_ub: array_like, optional 不等式约束的右侧值。A_eq: array_like, optional 等式约束的系数矩阵。每一行对应一个等式约束A_eq @ x == b_eq。b_eq: array_like, optional 等式约束的右侧值。bounds: sequence, optional 变量的界限，格式为(min, max) 对，可以为每个变量指定不同的界限。如果没有指定，默认为(0, None)，即非负约束。method: str, optional 指定求解器的方法。默认为 highs，这是 SciPy 1.5.0 之后推荐的方法。其他可选方法包括 ‘highs-ds’、‘highs-ipm’、‘interior-point’、‘revised simplex’ 等。options: dict, optional 传递给求解器的额外选项。
返回值linprog 函数返回一个优化结果对象，其中包含以下属性：x: array 最优解。fun: float 最优目标函数值。slack: array 不等式约束的松弛变量。con: array 等式约束的乘子。success: bool 表示是否成功找到最优解。status: int 表示求解器的状态。message: str 描述求解器状态的字符串。
注意事项linprog 默认解决的是最小化问题，如果需要最大化目标函数，应将目标函数系数取反。默认是小于等于，如果不等式出现大于等于，记得不等式两边要同时乘以-1确保约束条件是线性的。检查result.success 以确认是否找到了有效解。如果问题规模较大或约束条件复杂，可能需要调整method 和options 参数以获得更好的性能。

整数规划

数学规划中的变量（部分或全部）限制为整数时，称为整数规划。若在线性规划模型中，变量限制为整数，则称为整数线性规划。目前所流行的求解整数规划的方法，往往只适用于整数线性规划。目前还没有一种方法能有效地求解一切整数规划。

整数规划的特点

原线性规划有最优解，当自变量限制为整数后，其整数规划解出现下述情况

(1)原线性规划最优解全是整数，则整数规划最优解与线性规划最优解一致。
(2）整数规划无可行解。
(3）有可行解（当然就存在最优解），但最优解值变差。

整数规划最优解不能按照实数最优解简单取整而获得。

Topsis方法

评价方法大体上可分为两类，其主要区别在确定权重的方法上。一类是主观赋权法，多数采取综合咨询评分确定权重，如综合指数法、模糊综合评判法、层次分析法、功效系数法等。另一类是客观赋权，根据各指标间相关关系或各指标值变异程度来确定权数，如主成分分析法、因子分析法、理想解法去（也称TOPSIS 法）等。

目前已有许多解决多属性决策的排序法，如理想点法、简单线性加权法、加权平方和法、主成分分析法、功效系数法、可能满意度法、交叉增援矩阵法等。本节介绍多属性决策问题的理想解法，理想解法亦称为TOPSIS法，是一种有效的多指标评价方法。这种方法通过构造评价问题的正理想解和负理想解，即各指标的最优解和最劣解，通过计算每个方案到理想方案的相对贴近度，即靠近正理想解和远离负理想解的程度，来对方案进行排序，从而选出最优方案。

方法和原理

设多属性决策方案集为 $D = d_{1}, d_{2}, . . ., d_{m}$ ，衡量方案优劣的属性变量为 $x_{1}, . . . x_{n}$ 这时方案集D中的每个方案 $d_{i} (i = 1, . . . m)$ 的n个属性值构成的向量是 $a_{i 1}, . . ., a_{i n}$ ，它作为n维空间中的一个点，能唯一地表征方案 $d_{i}$ 。

正理想解 $C *$ 是一个方案集D中并不存在的虚拟的最佳方案，它的每个属性值都是决策矩阵中该属性的最好值；而负理想解 $C^{0}$ 则是虚拟的最差方案，它的每个属性值都是决策矩阵中该属性的最差值。在n维空间中，将方案集D中的各备选方案 $d_{i}$ 与正理想解 $C^{*}$ 和负理想解 $C^{0}$ 的距离进行比较，既靠近正理想解又远离负理想解的方案就是方案集D中的最佳方案；并可以据此排定方案集D中各备选方案的优先序。

算法步骤

TOPSIS法的具体算法如下：

用向量规划化的方法求得规范决策矩阵

设多属性决策问题的决策矩阵 $A = (a_{i j})_{m \times n}$ ，规范化决策矩阵 $B = (b_{i j})_{m \times n}$ ，其中

$b_{i j} = \frac{a_{i j}}{\sqrt{\sum_{i = 1}^{n} a_{i j}^{2}}}, i = 1, 2, . . ., m, j = 1, 2, . . ., n$

构成加权规范阵 $C = (c_{i j})_{m \times n}$

设由决策热给定各属性的权重向量为 $w = [w_{1}, w_{2}, w_{3}, . . ., w_{n}]^{T}$ ，则

$c_{i j} = w_{j \cdot b_{i j}}, i = 1, 2, . . ., m, j = 1, 2, . . ., n$

确定正理想解 $C^{*}$ 和负理想解 $C^{0}$

设正理想解 $C^{*}$ 的第j个属性值为 $c_{j}^{*}$ ，负理想解 $C^{0}$ 第j个属性值为 $c_{j}^{0}$ ，则

计算各方案到正理想解与负理想解的距离

计算各方案的排队指标值（综合评价指数）

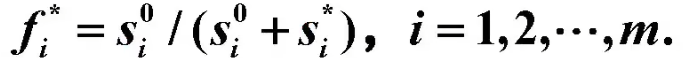
按 $f_{i}^{*}$ 由大到小排序方案的优劣次序